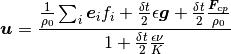Greyscale model¶
The LBPM greyscale lattice Boltzmann model is constructed to approximate the solution of the Darcy-Brinkman equations in grey regions, coupled to a Navier-Stokes solution in open regions. To use the greyscale model, the input image should be segmented into “grey” and open regions. Each particular “grey” label should be assigned both a porosity and permeability value.
A typical command to launch the LBPM color simulator is as follows
`
mpirun -np $NUMPROCS lbpm_greyscale_simulator input.db
`
where $NUMPROCS is the number of MPI processors to be used and input.db is
the name of the input database that provides the simulation parameters.
Note that the specific syntax to launch MPI tasks may vary depending on your system.
For additional details please refer to your local system documentation.
Model parameters¶
The essential model parameters for the single phase greyscale model are
tau– control the fluid viscosity –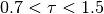
The kinematic viscosity is given by
Model formulation¶
A D3Q19 LBE is constructed to describe the momentum transport
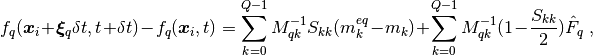
The force is imposed based on the construction developed by Guo et al
![$$
F_i = \rho_0 \omega_i \left[\frac{\bm{e}_i \cdot \bm{a}}{c_s^2} +
\frac{\bm{u} \bm{a}:(\bm{e}_i \bm{e}_i -c_s^2 \mathcal{I})}{\epsilon c_s^4} \right] ,
$$](../../../_images/math/e2232a69e808477fdf601c2be64e251c5825b7a7.png)
where 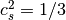 is the speed of sound for the D3Q19 lattice.
The acceleration includes contributions due to the external driving force
is the speed of sound for the D3Q19 lattice.
The acceleration includes contributions due to the external driving force 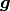 as well as a drag force due to the permeability
as well as a drag force due to the permeability 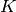 and flow rate
and flow rate 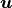 with the
porosity
with the
porosity  and viscosity
and viscosity 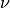 determining the net forces acting within
a grey voxel
determining the net forces acting within
a grey voxel
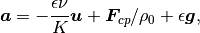
The flow velocity is defined as
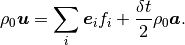
Combining the previous expressions,